Encryption is the method of turning plaintext into ciphertext using mathematical models or algorithms. It is at the core of password security and data security in general. This post is about a special, disruptive kind of encryption based on zero-knowledge proof. It’s an encryption scheme proposed in the 1980s by MIT researchers Shafi Goldwasser, Silvio Micali, and Charles Rackoff. We will discuss the mathematical foundation of zero-knowledge proof, its use cases across industries, and its role in transforming password encryption and cryptography in general.
In this article…
What is the zero-knowledge proof system?
The zero-knowledge proof system is a way for a prover to convince a verifier that a piece of information is true without revealing the said piece of information.
“A typical byproduct of proof is that you gained some knowledge,
other than that you are now convinced that the statement is true. A zero-knowledge proof tries to avoid it.“
Instead of looking for a strict mathematical proof, the verifier uses a statistical point of view to attain a probabilistic proof of authenticity. By asking the prover to perform a task that only the prover can perform repeatedly, the verifier decreases the probability of someone faking it.
Yes, it sounds a little complicated at the outset and it is very complicated on the inside. But that doesn’t mean we cannot look for an easier explanation.
A verifier, a prover, and a cave with two gates – Zero-knowledge proof explained
The example of a cave with two entry points with a locked door in between is used quite frequently to explain zero-knowledge proof or ZKP. It should help us build a basic understanding of the concept.
The image below depicts a cave with two gates, A and B. The path from A to B has a locked door in between. If someone wants to enter through gate A and exit through gate B, they would need the key to the door that blocks the way.
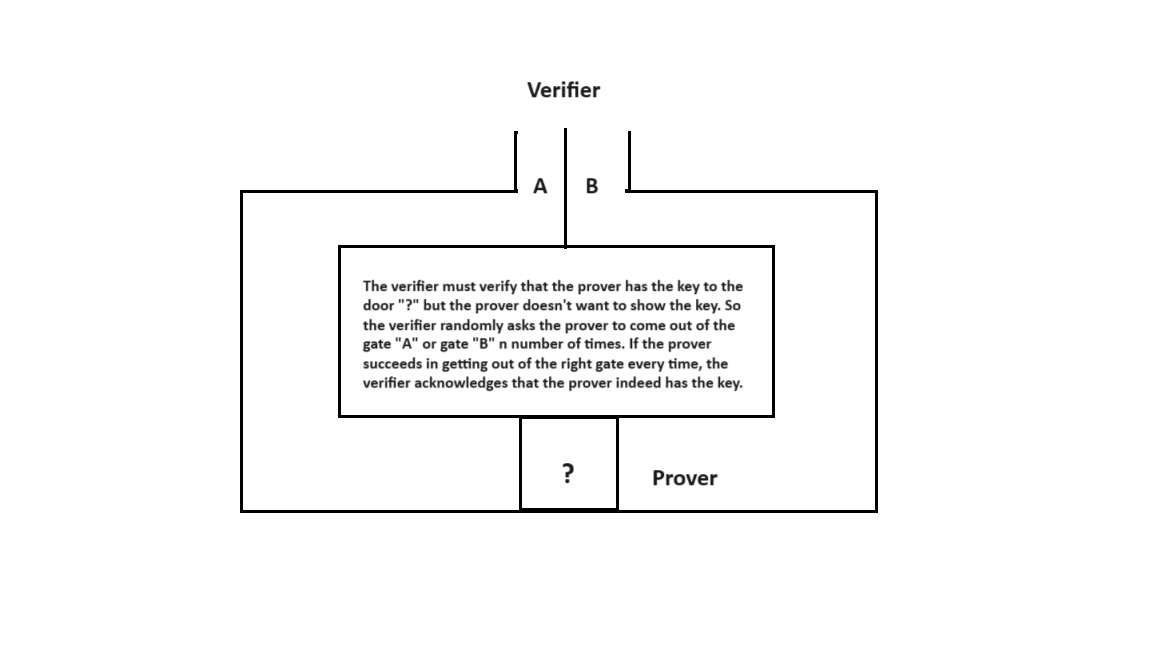
The verifier can ask the prover multiple times to enter and exit the cave through specific gates. If the prover succeeds in exiting through the right gate every time, it is statistically established that they have the key to the door.
3 key properties of zero-knowledge proof
- Completeness: The zero-knowledge proof system is comprehensive so it can convince the verifier that the prover has the knowledge it claims to have.
- Soundness: If the prover is dishonest, the verifier will not be convinced.
- Zero-knowledge: The verifier will gain no additional knowledge in the process of establishing that the prover has the knowledge it claims to have.
Two types of zero-knowledge proof
Interactive zero-knowledge proof
In this method, the verifier and the prover have to be in live contact for the prover to convince the verifier that the prover is the possessor of a piece of information also called the ‘witness‘.
Interactive zero-knowledge proof is a two-step mathematical process through which the prover establishes the possession of the witness without revealing it.
The issue with interactive zero-knowledge proof is that it requires live contact between the verifier and the prover and hence is not scalable. That is where non-interactive zero-knowledge proof comes in.
Non-Interactive zero-knowledge proof
Non-interactive zero-knowledge proof eliminates the need for live interaction between the two parties. The Fiat-Shamir heuristic, invented in 1986, made non-interactive ZKP1 possible. This method involves a hash function that randomly picks a verification challenge.
The mathematical foundation of zero-knowledge encryption
In this section, we’ll discuss the math underlying the zero-knowledge protocol. It is quite fascinating once you get the hang of it. So, here’s how zero-knowledge encryption works.
We’ll start by taking an
Integer g
A large prime P
and another integer y
Let's assume that these three are public knowledge and 0≤g<P, 0≤y<P, and 0≤x<P
Now, the prover wants to prove that he knows the value of x so that gxmodP=Y (example: 11mod4=3. 3 is the remainder when 11 is divided by 4)
So, if g = 3, P = 5, and y = 1, you need to prove that you know x where 3xmod5=1
This is called a discrete logarithm problem where to calculate x you need to try every possible value. In this case,
31mod5 = 3
32mod5 = 4
33mod5 = 2
34mod5 = 1
Therefore, The correct value of x is 4.While this was not very hard to calculate, if you increase the value of g and P significantly, even modern computers may take years to calculate the correct value of x. The probability of someone guessing the correct value of x is incredibly small.
If x is your password, the zero-knowledge protocol would allow you to prove to a verifier that you know x without revealing its value to them. This makes it possible for someone to log into their bank account without revealing their password. In 2016, researchers at Princeton University used ZKP to invent a method of determining if a weapon is nuclear without revealing any other information.
Verifying the zero-knowledge proof
If the password is known only to the prover then how can the verifier know if the password is correct? We can find that answer in the next part of the mathematical explanation.
Step 1. The prover takes a random integer (r) and calculates C where
C = grmodP
And sends C to the verifier.
Step 2. The verifier asks for the value of w where
w=x+rmod (P-1)
Step 3. At this point, the verifier knows g, P, y, C, and w.
If yCmodP = gwmodP
then, the prover has the right value for x.
Here’s how you can arrive at the above equation
yCmodP = gxgrmodP = gx+r modP = gx+rmod(p-1)modP
[According to Fermat’s Theorem, axmodP=axmod(P-1)modP when P is a prime.]
We already know that x+rmod(P-1) = w
Therefore, gx+rmod(p-1)modP = gwmodP
The key to maintaining the soundness and zero-knowledge nature of the protocol is that the verifier asks for either r or w randomly but never both. This prevents the prover from cheating and the verifier from determining the value of x.
Key benefits of zero-knowledge encryption
- The server doesn’t need the actual password to grant access to the authorized user therefore, it doesn’t store it. Even if the service provider faces a data breach, the passwords cannot be exposed, not even in encrypted form.
- Since the user never inserts the password into a user-input field, the chances of credential theft through a phishing attack are eliminated.
- It reduces data liability by reducing the amount of data a company needs to store
- It creates a secure way of transaction in situations where implementing end-to-end encryption is not feasible.
By comparing zero-knowledge encryption with other methods of encryption, one can easily validate its clear superiority in terms of privacy and data protection.
Primary use cases of zero-knowledge encryption
As a powerful cryptographic technique zero-knowledge encryption (ZKE) has been adopted by a wide range of industries including finance, blockchain, decentralized security, and identity management among others.
The ability to establish the possession of a piece of information without actually sharing the information gives the authentication process a cutting edge. From Zcash to secure voting systems, we’ll explore the evolving use cases of ZKE.
Secure digital identity verification
ZKE can be used to verify a user’s identity without revealing any sensitive personal information, such as their name, address, or social security number. This can help to protect user privacy and prevent identity theft.
Data protection
You can use ZKE for encrypting sensitive data, such as medical records, financial information, and trade secrets. For instance, ZKE can be used to prove to an insurance provider that a patient has undergone a specific treatment without revealing other sensitive medical data. Overall the role of zero-knowledge encryption in the evolution of data privacy is massive.
Secure transactions
ZKE can be used to prevent fraud in online payments while also protecting user privacy.
Privacy-preserving computation
ZKE enables privacy-preserving computation which allows two parties to perform computations on encrypted data without exposing the data to each other. This can be used for secure medical diagnosis and confidential business transactions while maintaining anonymity, privacy and security.
Enhanced blockchain security
ZKP or zero-knowledge proof can be used to hide the details of blockchain transactions while also ensuring the validity of said transactions. Zcash was the first cryptocurrency to implement zero-knowledge proof to create a private mode of transactions.
Secure voting systems
Zero-knowledge proof can be used to create a system where the validity of a vote can be established without revealing any additional information.
Privacy-preserving machine learning
ZKE can be used to enable privacy-preserving machine learning, which allows machine learning models to be trained on encrypted data without revealing the underlying sensitive information to the model developers or owners.
The above list is just the tip of the iceberg when it comes to the applications of zero-knowledge architecture. It is the future of authentication and identity management.
How does password encryption work?
When a user creates a password for an account, the server uses a hash function to transform the user input into a string of random characters with a fixed length and adds an arbitrary string to it (the process of adding the arbitrary string is called salting; it ensures that even if two user-generated passwords are identical, their encrypted forms are not).
The encrypted password is stored by the service provider. When the user tries to log in to that account using their password, the same hash function is applied to it. If it matches with one of the encrypted passwords, the user is granted access.
In the case of a password manager, the passwords stored in the vault are all encrypted and the decryption key is the master password known only to the user.
There are many different methods of encrypting passwords. There is symmetric encryption where the same key is used for encrypting and decrypting a piece of information and there is asymmetric encryption where a public key is used to encrypt data and a private key is required to decrypt it. We have discussed how password encryption works in detail in a different post.
Use of zero-knowledge proof at Uniqkey
Uniqkey is among the handful of access management solutions that use zero-knowledge architecture for securing your passwords.
It ensures that the encryption key or the master password you use to access the Uniqkey app never leaves your device and your identity is verified through a probabilistic approach. This system ensures that even if the password manager is hacked and breached, your data is unreachable.
Zero-knowledge security is just one of the host of cutting-edge features that make Uniqkey the perfect password manager for businesses. With automated employee logins, centralized access control, shadow IT monitoring, and complete administrative control, Uniqkey is the password management solution to beat in Europe, schedule a demo to learn more about Uniqkey.


